OWL 2 Profiles

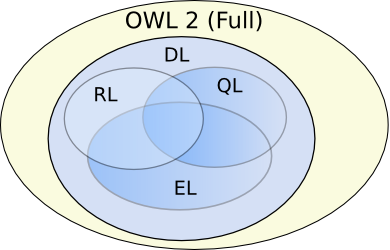
Reasoning Complexity

• OWL 2 Full: Undecidable
• OWL 2 DL: N2EXPTIME (2²ⁿ in the size of input)
• OWL 2 EL, OWL 2 RL, OWL 2 QL: Polynomial time

• They are used to test satisfiability (consistency)
• A tree (there can be loops) is built with nodes consisting of class expressions to be evaluated
• Edges are labelled with the relationships between classes
• Nodes are expanded by applying the tableaux rules
• Tree expansion stops when either no more rules can be applied or a clash occurs (for eg: $A \sqcap \neg A$)

• Apply Negation Normal Form on the given Knowledge Base K
• Apply tableaux rules on the axioms
• Check for termination
• If there is a contradiction in the tableaux, then it is unsatisfiable

• It simplifies the given knowledge base
• It is a syntactic transformation
• Initial steps
• Replace C $\equiv$ D with C $\sqsubseteq$ D and D $\sqsubseteq$ C
• Replace C $\sqsubseteq$ D with $\neg$C $\sqcup$ D
• Apply the NNF rules exhaustively
• In NNF(K), negation occurs only directly in front of atomic classes

• NNF(C) = C, if C is a class name
• NNF($\neg$C) = $\neg$C, if C is a class name
• NNF($\neg\neg$C) = NNF(C)
• NNF(C $\sqcup$ D) = NNF(C) $\sqcup$ NNF(D)
• NNF(C $\sqcap$ D) = NNF(C) $\sqcap$ NNF(D)
• NNF($\neg$(C $\sqcup$ D)) = NNF($\neg$C) $\sqcap$ NNF($\neg$D)
• NNF($\neg$(C $\sqcap$ D)) = NNF($\neg$C) $\sqcup$ NNF($\neg$D)
• NNF($\forall$R.C) = $\forall$R.NNF(C)
• NNF($\exists$R.C) = $\exists$R.NNF(C)
• NNF($\neg\forall$R.C) = $\exists$R.NNF($\neg$C)
• NNF($\neg\exists$R.C) = $\forall$R.NNF($\neg$C)

• Transform the axiom below to NNF
• P $\sqsubseteq$ (E $\sqcap$ M) $\sqcup$ $\neg$($\neg$E $\sqcup$ D)
• Step-1: $\neg$P $\sqcup$ ((E $\sqcap$ M) $\sqcup$ $\neg$($\neg$E $\sqcup$ D))
• Step-2: $\neg$P $\sqcup$ ((E $\sqcap$ M) $\sqcup$ (E $\sqcap$ $\neg$D))

• Input: Knowledge Base, K = TBox + ABox, in NNF
• Output: Whether or not K is satisfiable


• A tableau is a directed labelled graph
• Nodes are individuals or (new) variable names
• Nodes x are labelled with sets L(x) of class expressions
• Edges <x,y> are labelled with sets L(<x,y>) of role names

Initialization

• Make a node for every individual in the ABox
• Every node is labelled with the corresponding class names from the ABox
• There is an edge, labelled with R, between a and b, if R(a,b) is in the ABox
• If there is no ABox, the initial tableau consists of a node x with empty label

Initialization

• Build an initial tableau for the following knowledge base
• K = {A(a),($\exists$R.B)(a),R(a,b),R(a,c),S(b,b),(A$\sqcup$B)(c),$\neg$A$\sqcup$($\forall$S.B)}

Naive $ALC$ Tableaux Rules

• $\sqcap$-rule: If C $\sqcap$ D $\in$ L(x) and {C,D} $\not\subseteq$ L(x), then set L(x) $\leftarrow$ {C,D}
• $\sqcup$-rule: If C $\sqcup$ D $\in$ L(x) and {C,D} $\cap$ L(x) = $\emptyset$, then set L(x) $\leftarrow$ C or L(x) $\leftarrow$ D
• $\exists$-rule: If $\exists$R.C $\in$ L(x) and there is no y with R $\in$ L(x,y) and C $\in$ L(y), then
1. add a new node with label y (where y is a new node label),
2. set L(x,y) = {R}, and
3. set L(y) = {C}
• $\forall$-rule: If $\forall$R.C $\in$ L(x) and there is a node y with R $\in$ L(x,y) and C $\not\in$ L(y), then set L(y) $\leftarrow$ C
• TBox-rule: If C is a TBox statement and C $\not\in$ L(x), then set L(x) $\leftarrow$ C

Examples

• K = {C(a), C $\sqsubseteq$ $\exists$R.D, D $\sqsubseteq$ E}. Is ($\exists$R.E)(a) a logical consequence?
• K = {Human $\sqsubseteq$ $\exists$hasParent.Human, Bird(tweety)}. Is tweety not Human?


• Tableau constructed on whiteboard

Examples

• Try the following
  • Human $\sqsubseteq$ $\exists$hasParent.Human
  • Orphan $\sqsubseteq$ Human $\sqcap$ $\forall$hasParent.$\neg$Alive
  • Orphan(harrypotter)
  • hasParent(harrypotter, jamespotter)
  
  
  • Is $\neg$Alive(jamespotter), a logical consequence?

Blocking

• K = {$\exists$R.$\top$, $\top$($a_1$)}. Check the satisfiability of K
• Does the Tableau for K terminate?


• Tableau constructed on whiteboard


• Observation: Node x has the same properties of node $a_1$. So "reuse" $a_1$

Blocking

• Terms: Consider L(x,y) $\neq$ $\emptyset$. Let's say L(x,y) = {R}
• Successor: y is the successor (R-successor) of x
• Predecessor: x is the predecessor (R-predecessor) of y
• Ancestor: Every predecessor of y, which is not an individual, is an ancestor of y. Every predecessor of an ancestor of y, which is not an individual, is also an ancestor of y

Blocking

• A node with a label x is blocked by a node with label y if
• x is a variable but not an individual
• y is an ancestor of x, and L(x) $\subseteq$ L(y)
• or an ancestor of x is blocked

Naive $ALC$ Tableaux Rules (with blocking)

• $\sqcap$-rule: If C $\sqcap$ D $\in$ L(x) and {C,D} $\not\subseteq$ L(x), then set L(x) $\leftarrow$ {C,D}
• $\sqcup$-rule: If C $\sqcup$ D $\in$ L(x) and {C,D} $\cap$ L(x) = $\emptyset$, then set L(x) $\leftarrow$ C or L(x) $\leftarrow$ D
• $\exists$-rule: If $\exists$R.C $\in$ L(x) and there is no y with R $\in$ L(x,y) and C $\in$ L(y), then
1. add a new node with label y (where y is a new node label),
2. set L(x,y) = {R}, and
3. set L(y) = {C}
• $\forall$-rule: If $\forall$R.C $\in$ L(x) and there is a node y with R $\in$ L(x,y) and C $\not\in$ L(y), then set L(y) $\leftarrow$ C
• TBox-rule: If C is a TBox statement and C $\not\in$ L(x), then set L(x) $\leftarrow$ C
• Apply these rules only if x is not blocked

Blocking

• K = {$\exists$R.$\top$, $\top$($a_1$)}
• K = {Human $\sqsubseteq$ $\exists$hasParent.Human, Bird(tweety)}. Is tweety not Human?
• K = {hasChild(john,peter), hasChild(john,alex), Male(peter), Male(alex)}. Show that $\forall$hasChild.male(john) is not a logical consequence of K
• K = {Bird $\sqsubseteq$ Flies, Penguin $\sqsubseteq$ Bird, Penguin $\sqcap$ Bird $\sqsubseteq$ $\bot$, Penguin(tweety)}. Show K is unsatisfiable


• Tableau constructed on whiteboard