Ontology Reasoning
Monsoon 2018
Instructor: Raghava Mutharaju
IIIT-Delhi

Ontology Reasoning
- Reasoning is the process of deriving facts that are not explicitly expressed in the ontology
- Reasoning makes implicit facts explicit
- Logical consequences are drawn from the axioms in the ontology
Ontology Reasoning
- Axioms before reasoning
- {john} $\sqsubseteq$ USCitizen
- USCitizen $\sqsubseteq \exists$hasPassport.USPassport
- $\exists$hasPassport.USPassport $\sqsubseteq$ EUVisaNotRequired
- Logical consequences after reasoning
- USCitizen $\sqsubseteq$ EUVisaNotRequired
- {john} $\sqsubseteq$ EUVisaNotRequired
Purpose of Ontology Reasoning
- Design and maintain high quality ontologies
- Consistency: reasoner helps in determining whether an ontology is consistent or not
- Minimally redundant: reasoner checks for unintended synonyms
- Answer queries over ontology classes and instances
- Find more general/specific classes
- Retrieve individuals of a class
Expressivity and Complexity Trade-off
OWL 2 Profiles
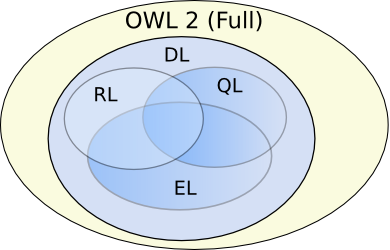
Reasoning Complexity
- OWL 2 Full: Undecidable
- OWL 2 DL: N2EXPTIME (22n in the size of input)
- OWL 2 EL, OWL 2 RL, OWL 2 QL: Polynomial time
Types of Reasoning
- Forward chaining
- Start with the axioms and apply inference rules repeatedly until no more new axioms can be derived
- Saves time during querying but ends up using more space
- Backward chaining
- Start with a query and apply inference rules that are needed to only answer the query
- Saves space but increases the querying time
Important Reasoning Tasks
- Consistency of the knowledge base (ontology in our case)
- Class level consistency (is class C empty, $C \equiv \bot$)
- Class inclusion (is class C a subclass of class D)
- Class equivalence
- Class disjointness
- Class membership (does an instance a belong to class C?)
- Instance retrieval (list all the instances of class C)
Reasoning Procedure
- Rule based reasoning
- Tableaux algorithm
Rule based reasoning
- If $X \sqsubseteq A$ and $A \sqsubseteq B$ then $X \sqsubseteq B$
- If $X \sqsubseteq A_1$ and $X \sqsubseteq A_2$ then $X \sqsubseteq A_1 \sqcap A_2$
- If $A \sqsubseteq \exists r.B$ and $\exists r.B \sqsubseteq C$, then $A \sqsubseteq C$
- If $A \sqsubseteq \exists r.B$, $B \sqsubseteq C$ and $\exists r.C \sqsubseteq D$, then $A \sqsubseteq D$
- If $A \sqsubseteq \exists r.B$, $r \sqsubseteq s$ and $\exists s.B \sqsubseteq C$, then $A \sqsubseteq C$
- If $A \sqsubseteq \exists r.B$, $r \sqsubseteq s$, $B \sqsubseteq C$ and $\exists s.C \sqsubseteq D$, then $A \sqsubseteq D$
Tableaux Algorithm
- They are used to test satisfiability (consistency)
- A tree is built with nodes consisting of class expressions to be evaluated
- Edges are labelled with the relationships between classes
- Nodes are expanded by applying the tableaux rules
- Tree expansion stops when either no more rules can be applied or a clash occurs (for eg: $A \sqcap \neg A$)
References
- OWL 2 Profiles. Boris Motik et. al. 2012